Professor Roger H. Rangel
Graduate Student: Ruth A. Lambert
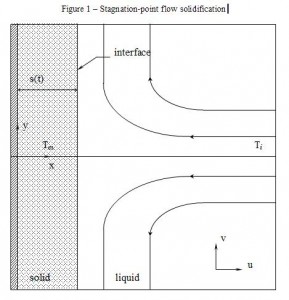
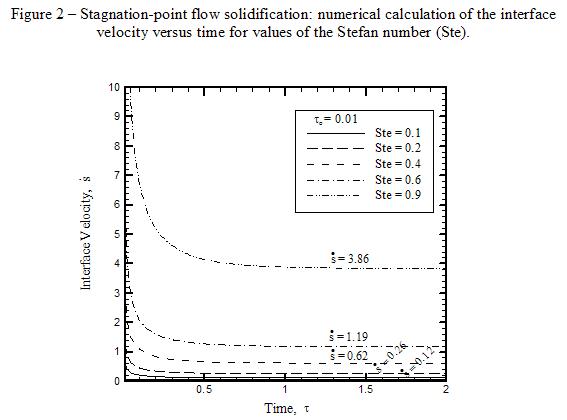
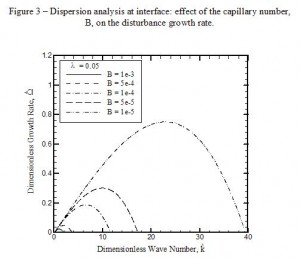
Analytical analyses of the solidification process of a supercooled liquid in a half-space provide further insight into classical solidification problems and crystal growth theory. Under consideration are the cases pertaining to stagnation-point flow in the liquid phase and instability at the solid-liquid interface, with and without convective effects. The posed problems involve a phase change with a moving boundary at the solid-liquid interface. A classical solution exists for the case of solidification of a supercooled liquid in the absence of convection. Previous research shows that the onset of crystal growth can be predicted by the growth of a disturbance introduced at the solid-liquid interface. The solution of the unsteady temperature profile and the development of the solid region is found using numerical methods to solve the energy transport equation. The position of the solid-liquid interface is found using the heat-balance equation. The results show that after a long time the velocity of the solid-liquid interface approaches a constant value and the temperature field reaches a quasi-steady state. The quasi-steady temperature field is used to develop the governing equations of a linear perturbation analysis in the presence of stagnation-point flow. A linear perturbation analysis, including a complete dispersion analysis, is conducted for the case of solidification in the absence of convection, including the effects of surface curvature. The results show that the capillary effect increases interface stability, within the limits of large surface curvature, while thermal gradients have a destabilizing effect.
References
- R.A. Lambert and R.H. Rangel, “Linear stability analysis of the solidification of a supercooled liquid in a half-space”, International Journal of Heat and Mass Transfer, No. 45, 4577-4587, 2002.
- R.A. Lambert and R.H. Rangel, “Solidification of a supercooled liquid in stagnation-point flow”, International Journal of Heat and Mass Transfer, No. 46, 4013-4021, 2003.
Figures