Liquid Metal Droplet Deposition with Substrate Remelting

Professor Roger H. Rangel
Assistant Specialist: Xiaoli Bian

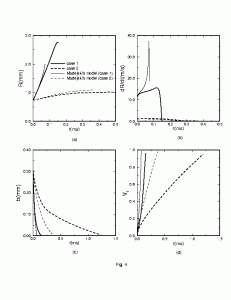
Metal droplet deposition is an important process with several applications in manufacturing. Some of these applications are encountered in spray and plasma-spray deposition, and in microcasting and net-shape manufacturing. When a molten droplet arrives at the substrate, it undergoes deformation and solidification. The rates of deformation and solidification are, in general, of the same order of magnitude, so it is important to be able to predict the coupled behavior involving fluid deformation, heat transfer, and solidification. Typical existing models have either neglected the deformation by assuming that it takes place fast or have used prescribed solutions of the solidification problem decoupled from the fluid dynamics. The present work describes a model of droplet deformation and solidification which includes a solution of the mechanical energy equation containing kinetic and potential energy as well as viscous dissipation. In addition, the transient, convective-diffusive energy equation including viscous dissipation is solved in the deforming liquid phase by means of finite differences after appropriate coordinate transformations. The solid phase transient energy equation is also solved in a transformed domain, and the liquid and solid solutions are coupled to predict the actual growth of the solidification front. Because the solid energy equation is solved in the complete domain, which includes the substrate, it is possible to predict the conditions for remelting of the substrate. Parametric studies are presented for a variety of relevant processing parameters.

References

Figures

Fig. 1 Time evolution of the splat shape formed by liquid aluminum droplet impinging on a cold substrate (red = liquid, blue = solid).
Fig. 1 Time evolution of the splat shape formed by liquid aluminum droplet impinging on a cold substrate (red = liquid, blue = solid).
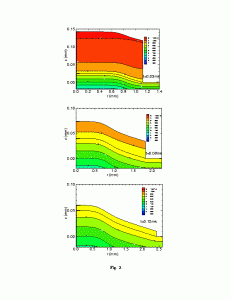
Fig. 2 Temperature field in the splat and upper substrate at selected times formed by liquid aluminum impinging on a cold substrate.
Fig. 2 Temperature field in the splat and upper substrate at selected times formed by liquid aluminum impinging on a cold substrate.

 

Fig. 3 Time evolution of the splat shape formed by liquid aluminum droplet impinging on a hot substrate (with remelting).

Fig. 3 Time evolution of the splat shape formed by liquid aluminum droplet impinging on a hot substrate (with remelting).

 

 

Fig. 4 Time evolution of (a) splat radius, (b) radius expansion rate, (c) liquid thickness, and (d) solid fraction for droplet impinging on cold substrate ( case 1: with high impinging velocity, and case 2: with low impinging velocity).
Fig. 4 Time evolution of (a) splat radius, (b) radius expansion rate, (c) liquid thickness, and (d) solid fraction for droplet impinging on cold substrate ( case 1: with high impinging velocity, and case 2: with low impinging velocity).