My research interests focus on the three fields: finite element methods , inverse problems and deep learning.
Finite Element Methods
Particularly, I am interested at designing special finite element methods (FEM) for solving interface problems on unfitted meshes. Interface problems arise from application that involve multiple media/materials with distinct physical or chemistrical properties, for example the left one below. Traditional FEM must be used on interface-fitted meshes, such as the one shown below on the middle, for optimal convergence. Generating interface-fitted meshes is generally expensive which is even more troublesome for moving interface problems. So it would be desirable for solving interface problems on unfitted mesh such as the one shown in the right plot below.

- Immersed Finite Element (IFE) Methods: I have been working on the IFE methods, and the idea is to encode the jump information on the interface to the construction of IFE functions. The non-conventional shape functions in IFE methods are usually piecewise polynomials shown in the right plot above.
- Virtual Element Methods (VEM): Recently, I am also interested at the VEM, and the idea is not to perform triangulation near the interface but use various shaped polyhedron as the elements in the mesh. As the remarkable advantage, this approach circumvents the triangulation requiring the maximal angle condition which is the key difficult for 3D meshes.
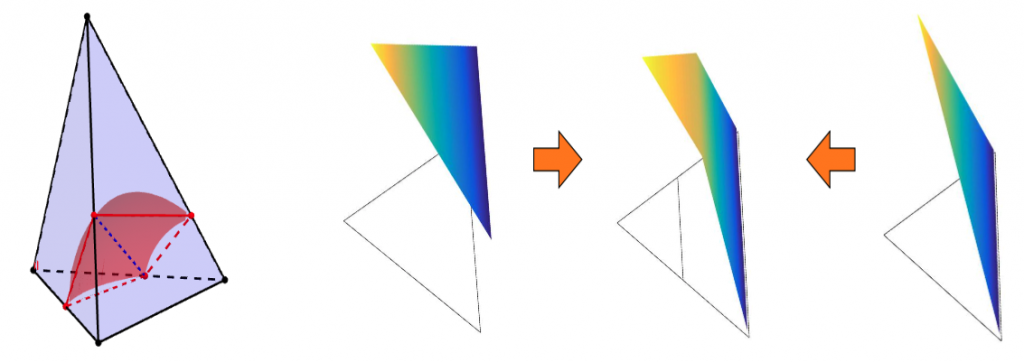
Top: fitting an interface by two polyhedra. Right: a 2D IFE functions formed by piecewise polynomials.
Inverse Problems
I am also interested at boundary value inverse problems that use data collected only at the boundary to recover the properties of internal media, including but not limited to the following problems
- Electrical Impedance Tomography (EIT): This technology uses the electrical potential and flux data on the boundary for reconstructing internal media distribution.
- Diffuse Optical Tomography (DOT): In this technology, the input flux of near-infrared (NIR) photons is used to illuminate the body and the output flux is measured on the surface of the body. Then, the input and output flux are used to recover the optical properties.
- Elastography: the displacement fields caused by the applied stress on the boundary are measured to detect the changes of mechanic properties inside tissue.
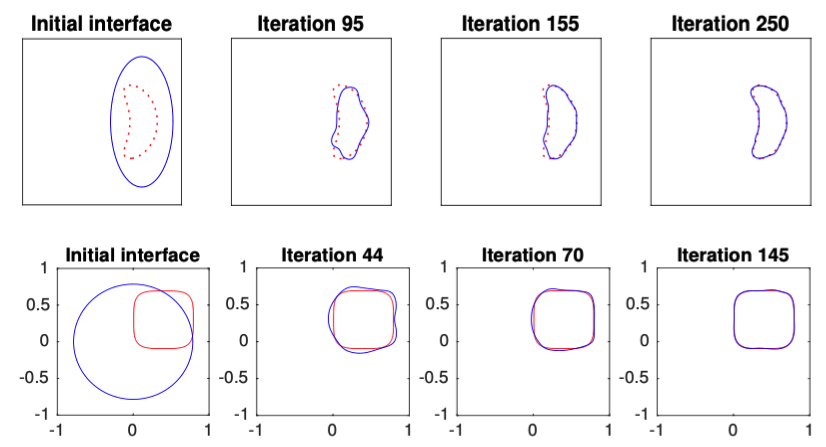
Mathematically, these problems can be formulated as recovering the interface which is the boundary of some inclusions occupied by distinguished media, and it becomes a family of geometric inverse problems. Shape optimization methodology is very popular for solving those geometric inverse problems. The idea is to minimize a data-misfitting functional that generates a sequence converging to the exact coefficient. The two plots above are example how the numerical interface converges to the exact one.
Deep Learning
My recent research interests focus on deep learning (DL) algorithms. In particular, I have been extensively working on using neural networks to learn operators and the application of operator learning to inverse problems. Our researches reveal that the concept of operator learning has great potential in efficiently and accurately solving challenging inverse problems, which significantly outperforms many conventional methods.
The essential reason is that the deep neural network architecture is able to capture the high-dimensional non-linear mathematical structure of inverse operators, while it is generally very difficult to derive a closed form of those operators by classical mathematical approached.
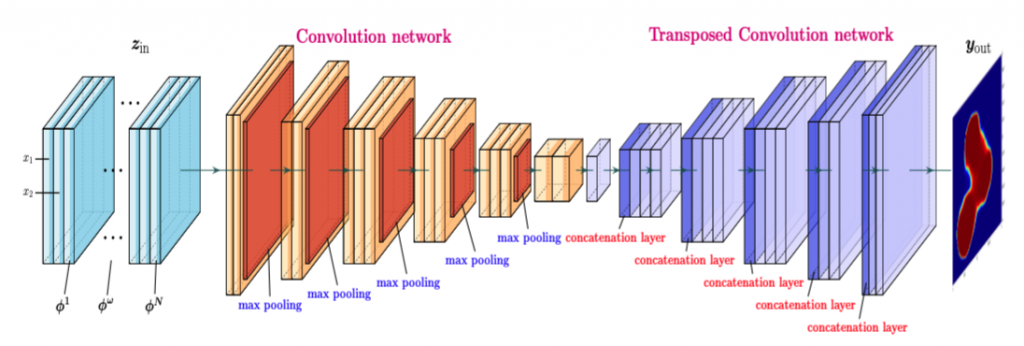
Currently, I have been working on a so called deep direct sampling method (DDSM) that combine the classical mathematically-profound estimate for the inverse operator and the DL algorithm. It has been successfully applied convolutional neural network (CNN) to learn the inverse operators from EIT and DOT.


