Professor Roger H. Rangel
Assistant Specialist: Xiaoli Bian
Stagnation-Flow Solidification Models
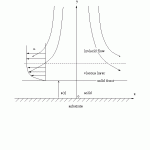
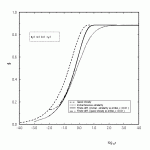
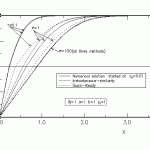
Transient heat transfer problems involving melting or solidification are important in many engineering applications involving processes such as casting, welding and spray forming. The problem of solid-liquid phase change belongs to the class of moving boundary problems because of the existence of a moving interface. The rate of propagation of this boundary into the liquid region (solidification) or into the solid region (melting) depends on the thermal properties of the solid and liquid regions, and in addition, in the cases where there exists motion in the liquid phase, such as metal droplet solidification in spray processes, it also depends on the fluid and flow properties of the liquid region. In our study, the effect of the liquid motion on its solidification behavior has been investigated by considering the two-dimensional stagnation flow onto a cold substrate. By coupling liquid-phase momentum equation and the conductive-convective liquid energy equation with the heat conduction equation in the solid region as well as the energy balance equation at the interface, we set up the mathematical model of the half space convective Stefan solidification problem. An instantaneous-similarity method and a quasi-steady method, as well as the finite-difference method have been applied to solve the time-dependent system of equations. Parametric studies such as the effect of Prandtl number, Stefan number, the stagnation-flow flow strain rate, and the ratio of the liquid and solid phase thermal diffusivity, as well as the initial substrate and liquid phase temperatures on the solidification behavior have been conducted. The solution provides a more reasonable model for the solidification behavior of the liquid in motion, and provides better insight into situations such as those encountered during the deformation and solidification of a droplet impinging on a cold substrate.
References
- Rangel, R.H. and Bian, X., “The Inviscid Stagnation-Flow Solidification Problem“, Int. J. Heat Mass Transfer, 39, No. 8, 1591-1602, 1996.
- Rangel, R.H. and Bian, X., “Numerical Solution of the Inviscid Stagnation-Flow Solidification Problem“, Numerical Heat Transfer-Part A: Applications, 28, No. 5, 589-603, 1995.
- Bian, X. and Rangel, R.H., “The Viscous Stagnation-Flow Solidification Problem“, Int. J. Heat Mass Transfer, No. 17, 3581-3594, 1996.
- Bian, X. and Rangel, R.H., “Stagnation-FLow Solidification on a Finite Thickness Substrate“, Int. J. Heat Mass Transfer, 1997.
Figures